October 2013
The relationship between light speed energy and the kinetic energy of non-relativistic particles is considered and an equation proposed to unify them. This leads naturally to the postulation of the de Broglie vector to represent any relativistic or non-relativistic particle. By adopting this concept, it is possible to account for the wave-particle duality associated with quantum mechanics, which is demonstrated here for both diffraction and refraction. The angular momentum of the de Broglie vector can be considered as the spin of a particle, pointing along the axis of rotation. The visualisation of a particle as simply a de Broglie vector leads to the idea that all matter is an embodiment of energy trapped within a potential well. If a photon escapes the potential well and reacts in a negative manner to the gravitational field of the potential well, it would reach the speed of light almost instantaneously.
There is no reason to suppose that there is any essential difference between space and matter. Nor is there any reason to suppose that matter and energy are not simply two embodiments of the same thing.
Ever since Einstein proposed the theory of Special Relativity [1], there has been a dichotomy between relativistic phenomena and those of the Newtonian world. In an earlier paper [2], Einstein proposed the existence of the photon. This paved the way for quantum mechanics, which eventually led to the problem of wave-particle duality. In a subsequent paper [3], Einstein proposed his famous relationship between energy and mass. In this paper we try to rationalise the relationship between matter and energy by proposing an equation that applies to all particles, including photons. The natural progression from this equation is the concept of a de Broglie vector rotating in de Broglie space.
The conundrum of wave-particle duality has long been reported in even the most elementary of texts (e.g. [4]). Wavelike properties are required to account for diffraction and refraction. The difficulty has always been associated with the fact that individual particles behave like particles, but the average behaviour of a large number of particles resembles that of a wave. We show that, because the de Broglie vector factorises into two components, anti-phase in the de Broglie plane, it is possible to consider the two components as acting in a manner that would produce results identical to a wave function.
Even electrically neutral particles, such as the neutron, have a magnetic moment of spin [5]. It is normally accepted that the spin of such a particle is not related to its physical rotation in space. In this paper, we conjecture that the de Broglie vector, rotating in de Broglie space could account for the spin of such a particle.
Michelson and Morley [6] observed that the speed of light was constant for all observers, at least in the same frame of reference. Kennedy and Thorndyke [7] later verified that there was no observed change in the measured speed of light when the surface of the Earth travels in different directions. However, there is no conclusive theory to establish why the speed of light is c rather than some other value, nor to describe why its value appears to remain constant, at least to all observers in the same reference frame. In this paper we suggest that a photon ejected from within the Schwarzschild [8] radius of a particle would accelerate to c in an immeasurable short time and distance if it were subjected to a negative gravitational effect.
If we consider a particular photon as a quantum of pure energy, we denote its energy e by the well known expression [9]
Where h is Planck's constant and f is the characteristic frequency associated with that particular photon. Now from basic wave theory we can define the frequency, f, by
So
or
Now there is an equivalence between energy and mass via Einstein's well known equation [3].
Where m is the rest mass of a physical entity. In this analysis, we use the term mE to indicate that the photon has no mass but mE is its mass equivalence. We now have
Rearranging we get
In eq. 2.7, λ is the Compton wavelength of a physical particle with rest mass mE. This reminds us of the expression for the de Broglie wavelength of a physical particle with rest mass mE and velocity of magnitude v
Now we can define the de Broglie frequency, fdB, via
Which leads to
In other words
But remembering that, for a physical particle
We expect to arrive at
So, there is a question as to how we can reconcile eq. 2.1 with eq. 2.13. We surmise that both could be written as
It can be seen that when v = c, this equates to eq. 2.1, whereas when v ≪ c, it equates to eq. 2.13. Combining eq. 2.14 with eq. 2.11 we have
Here we hypothesise that every particle with a de Broglie wavelength can be represented by a directional de Broglie vector, rdB, which rotates with rotational velocity vdB, where rdB and vdB are orthogonal in de Broglie space, such that
So we can rewrite eq. 2.15 as
Which, because rdB rotates in de Broglie space, can be factorized to
So we can rewrite eq. 2.15 as
Equation 3.3 suggests that we can consider any particle as the convolution of two separate components, each of which is a vector sum, with the imaginary parts anti-phase. Now if one component is phase-shifted by π then eq. 3.3 becomes
Which expands to
Now the middle term in the brackets of eq. 3.4 is imaginary in real space, so we are left with
For photons travelling at light-speed, |v| = |vdB| , so e becomes zero and there would be extinction at any angle where there was such a phase shift. For other, sub light-speed particles, there would be a minimum but not extinction because |v| > |vdB|. Equation 3.4a is useful when considering diffraction.
Now, if we consider |vdB| = ω|rdB|, where ω is the rotational velocity in radians per second and rdB is the de Broglie vector, we can calculate the amplitude of the de Broglie vector using ω = 2 π fdB, where fdB is the de Broglie frequency. From eq. 2.11
Therefore, using the substitution of eq. 3.1, we have
So the amplitude of the de Broglie vector, |rdB| is given by:
Which reduces to:
Note that the expression for |rdB| is identical to that for the reduced Compton wavelength for a physical particle with rest mass mE and is independent of the frame of reference of any observer. It can therefore be regarded as the de Broglie signature of a particle, whether a physical particle or a photon.
Wavelike properties are required to account for diffraction and refraction. The difficulty has always been associated with the fact that individual particles behave like particles, but the average behaviour of a large number of particles resembles that of a wave.
By describing a particle as a de Broglie vector rotating in de Broglie space it becomes clear that both the classical concept of a particle and the quantum mechanical description of a particle as a wave packet can be unified within a single model. It is no longer necessary to describe a particle as two different manifestations, depending on the situation.
The simplest case used to demonstrate this behaviour is the double slit experiment, shown in fig 4.1. Each particle can be detected at the detector as a discrete event.
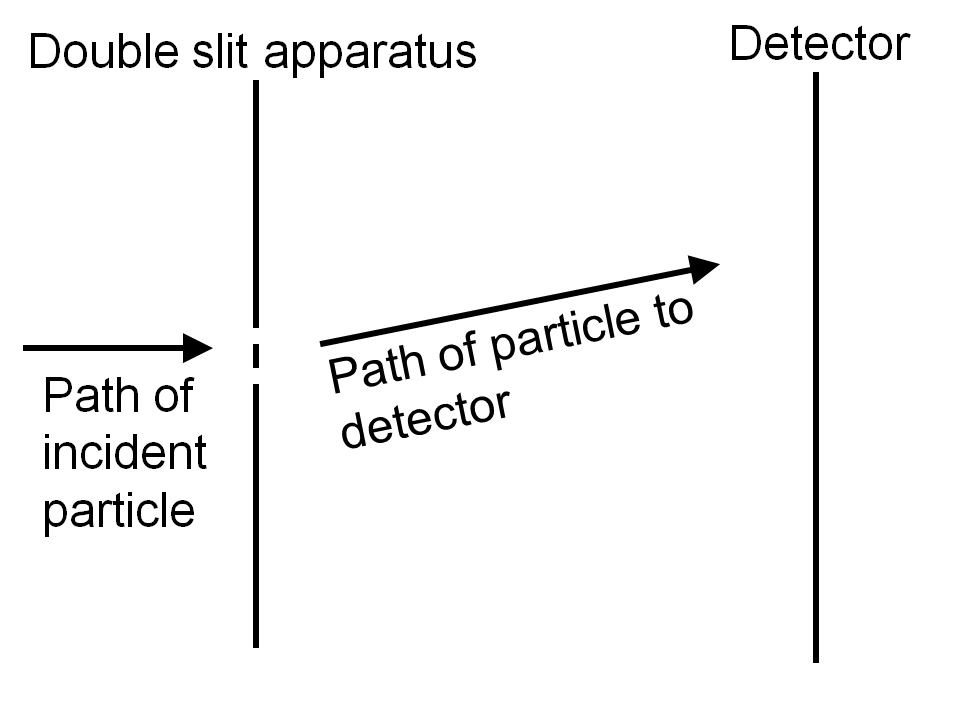
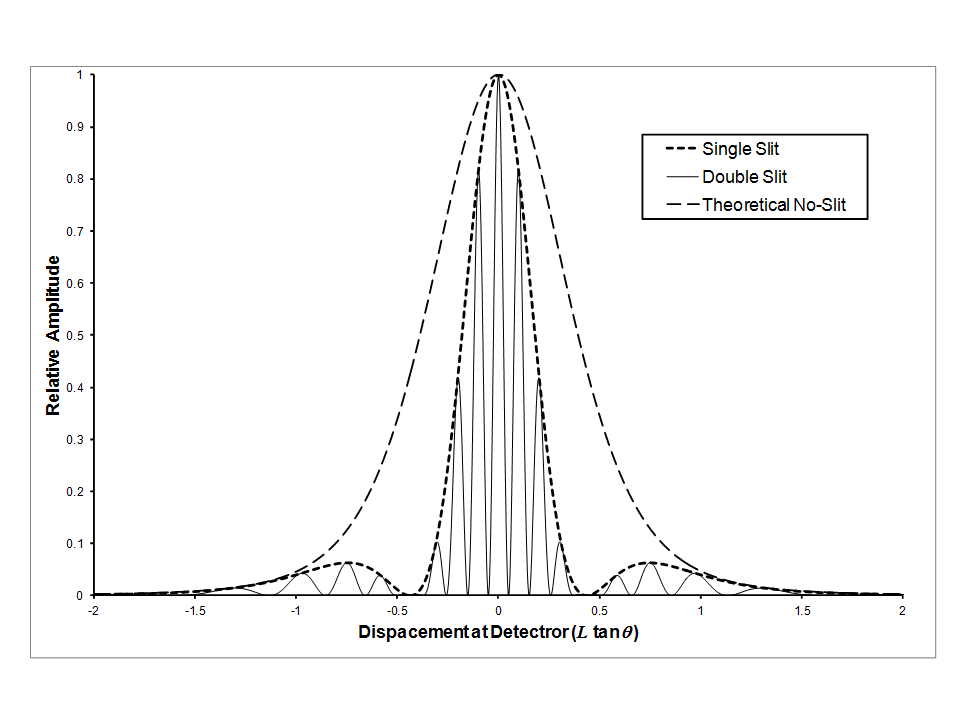
Before we consider the double slit experiment, we should also consider the single slit situation and a theoretical "no slit" experiment. In this thought experiment, we define the source of particles as a point source, the slit apparatus as a plane normal to a line drawn from the source to the apparatus and the detector as a linear array arranged in a line normal to the plane of the slit projected through the source. Each particle can be detected at the detector as a discrete event at an angle θ to a line drawn from the source to the slit. It is usual to think of the particles as photons, with the slit apparatus constructed of a material opaque to visible light. Also, electrons are often considered, with the slit apparatus constructed of a material impervious to electrons. However, other particles, such as neutrons, can also be considered if the slit apparatus is impervious to them. In the case of neutrons, suitable materials would be cadmium or BF4. The expected results from a beam of particles can be visualised by means of fig. 4.2.
The question arises as to how independent particles, each of which is recorded as a discrete event at the detector, can somehow collaborate to form a wavelike pattern. Additionally, if an attempt is made to discover through which slit each particle passes, the wavelike effect disappears. This is usually accounted for by citing the Heisenberg uncertainty principle, but without any attempt to explain how the slit measurement interferes with the experiment.
We assume that a quantum particle can be represented by nothing more than the de Broglie vector and a probability function in space. For the purpose of our thought experiment, it is sufficient to reduce the probability function to a single dimension, as shown in fig. 4.2. Because the detector is linear but the outputs from the slit apparatus emerge at an angle θ, the displacement from the centre line recorded at the detector will be L tanθ, where L is the distance from the slit apparatus to the centre line of the detector along a line drawn from the source.
The theoretical no-slit distribution represents the relative probability of an individual particle arriving at any point along the detector if there were no phase effects. Note that, in this case, the overall probability of transmission by the apparatus is 1. The theoretical no-slit distribution therefore determines the exit angle, θ, of the particle from the apparatus relative to a straight line path. A suitable probability function would be
Although there can never be any direct evidence of the results from a purely theoretical experiment, the probability can be inferred from the diffraction patterns from the single and double slit experiments because the observed results depend on the convolution of a sine wave probability and the probability defined in eq. 4.1. The value of a in eq. 4.1 can be chosen to adjust the half-height half-width of the probability function. For the purposes of this thought experiment, the value of a has been chosen to be 5.
In the case of the single slit apparatus, it is normal to use a wave theory approach, where λ is the wavelength of the wave function. The geometry is shown in fig. 4.3, with W the slit width and λ the wavelength. For this thought experiment we have used W = 2.5.
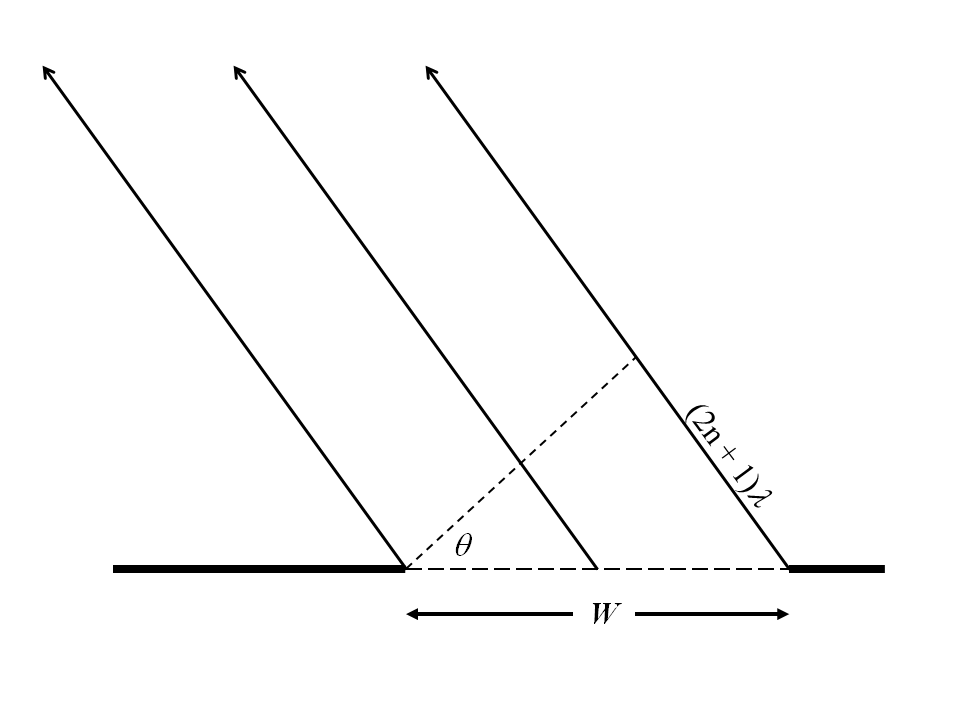
It is deduced that for any non-negative integer n, when (2n + 1)λ = W sin θ, the phase of the wave function from the centreline of the slit will be anti-phase to the phase at the edges, so that the signal will cancel. However, for a single particle, the wave theory approach is inappropriate. It would be more acceptable to define a new probability function for the transmission of the particle by the apparatus, based on the de Broglie wavelength of the particle. We need to have the probability of transmission equal to 1 when sin θ = 2nλdB/W and the probability of transmission equal to 0 when sin θ = (2n + 1)λdB/W. Equation 4.2 defines such a probability because π(W/λdB)sinθ evaluates to 2nπ in the former case and (2n + 1)π in the latter. If θ is identical to that used to define eq. 4.1, this fits with the wave theory approach, but can be also applied to a single particle.
PT(S) is the probability of transmission by the single slit apparatus and describes a sine wave with a maximum probability of 1 and a minimum probability of zero. In order to produce the observed single slit diffraction pattern, PS(θ), it is necessary to convolute this with P(θ) to produce the overall probability that a particle will be detected at any point along the detector, as shown for the single slit pattern in fig. 4.2. So
Figure 4.4 illustrates the double slit experiment, with d the separation between the slits, θ the angle of deflection, n a non-negative integer and λdB the de Broglie wavelength of the quantum particle. For this thought experiment, we have used d = 10λdB.
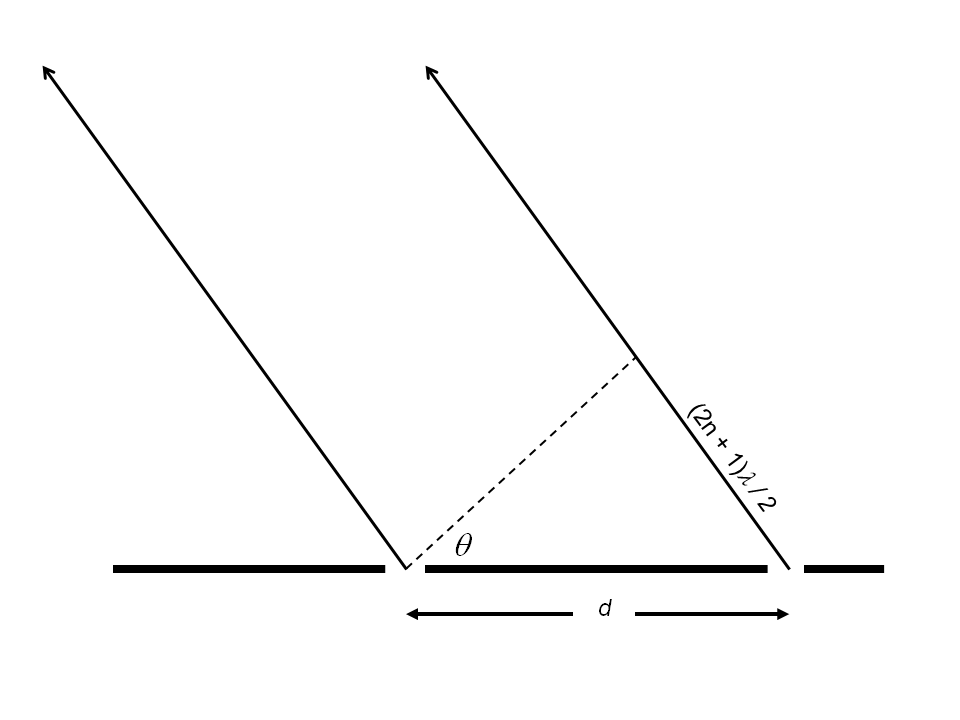
In order to explain the double slit experiment in purely quantum mechanical terms it is useful to abandon the idea that a particle passes through only one slit. So the de Broglie vector of the particle may be regarded as having two components, defined in eq. 3.3, one from each slit. Now the particle may reach the detector at any point defined by a new probability function associated with each slit (eq. 4.3). However, at an angle θ, such that
the de Broglie vector from the two slits will be anti-phase. In eq. 4.4, n is a non-negative integer, λdB is the de Broglie wavelength and d the inter-slit distance. In that case the particle will be transmitted with a probability zero. On the other hand if
the de Broglie vector from the two slits will be in phase and the particle will be transmitted with a probability of 1. More formally, using a similar argument as for the single slit, we can express the probability, PT(D), as
By convoluting PT(D) with the probability defined by eq. 4.3 we arrive at
PD(θ) is shown as the double slit result in Figure 4.2. Detecting the slit through which the particle passes reduces the scale of detecting to that of a single slit. It probably does so because if the particle is detected at one of the slits, the component of the de Broglie vector from that slit will be compromised and only the component from the other slit will pass through the slit apparatus. Hence a detected particle will have its directional probability collapsed to a single slit and therefore the de Broglie vector will have only a single component. Thus the distribution at the detector will be reduced to that of a single slit.
If a particle can be regarded as a de Broglie vector rotating in de Broglie space, then as it approaches the boundary between two media there will be two extremes of phase, one closest to the boundary and one furthest from it. Here we assume, without proof, that the speed of the particle depends on the nature of the medium in which it is travelling, which is the wave theory assumption associated with Snell's law.
If we consider the two components of eq. 3.3, we can approximate a quantum particle as two particles represented by Pa and Pb with separation of twice the de Broglie amplitude, 2rdB, as shown in fig. 4.5. For convenience, we have used x to represent 2rdB.
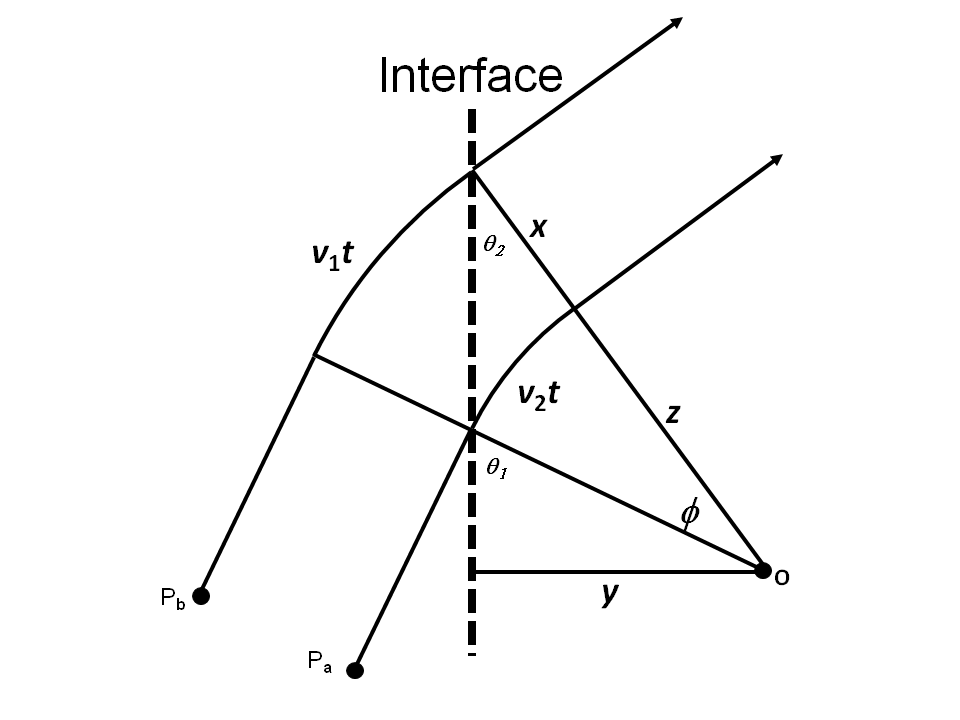
We use the following argument to show that the quantum particle will satisfy Snell's law. Assume that the separation between the particles is x and the speeds of the particles in the incident and emergent media are v1 and v2 respectively. When Pa crosses the interface, its speed will be reduced to v2, whereas Pb will continue to travel at v1 until it reaches the interface. If the particles continue with a separation of x, they will describe the curved path around the point O, as shown in Figure 4.5. After Pb crosses the interface they will travel in a straight line once again. If Pb reaches the interface t seconds after Pa, it can be seen that
and
Hence
So
Now
and
so
From eq. 4.14 and 4.11 we arrive at
The analysis is completely independent of x, the inter-particle separation, which is effectively twice the amplitude of the de Broglie vector. Thus it can be demonstrated that, if a quantum particle is regarded as a de Broglie vector rotating in de Broglie space, it will obey Snell's law without recourse to wave-particle duality.
Because vdB and rdB are orthogonal, the angular momentum, L, for the de Broglie vector is given by
so
This simplifies to
In the normal manner, L points along the axis of rotation of the de Broglie vector. Now for a photon, where v = c
Where v < c, the requirements for conservation of linear momentum and conservation of energy mean that for particles that coalesce or particles subject to decay, the magnitude of v will be the same for all particles taking part in the reaction. So, if we regard L as the spin of a particle, then in all cases spin will be conserved.
It has long been the custom to express the rest mass of a particle in terms of its energy equivalence via e = mc2. The invariance of rdB demonstrated by eq.3.8 suggests that it might be more appropriate to express the mass of a particle in terms of rdB :
Indeed it might be helpful to consider matter as simply captured energy trapped within a potential well. This would fit very well with a model where photons react to a gravitational field in a negative manner. That is to say they are repelled by matter rather than attracted to it. This would mean that, if a photon were to escape from a potential well, it would accelerate away from the relatively large positive mass of the potential well. Now the force, F, between two masses in a gravitational field is characterised by
Where G is the gravitational constant, m1 and m2 the two masses and r the separation between them. Thus, if a particle with negative mass had a mass several orders of magnitude smaller than that of a positive mass, m, the acceleration, a, of the negative particle is given by
We can find the radial velocity, v, of such a particle at a distance, r, from the positive mass, starting with an initial zero radial velocity at a distance r0 from the mass, by taking the integral of both sides of eq. 6.3 to give
Writing
we get
If the maximum value of v is c, the speed of light, this gives
It is interesting to note that this is exactly the Schwarzschild radius of the mass. For a mass of the order of a proton, r0 = 2.48 × 10-54 m, which is an extremely small distance. When r is less than r0, v becomes imaginary, so r0 might be considered as the limit of a potential well. On ejection, the radial velocity of a photon would accelerate to .99999999c by the time it reached 10-45 m from the centre of the potential well.
A photon approaching a physical particle would be decelerated as it approached within, say 10-40 m of the particle with its speed reduced to zero at the boundary of the potential well. From there it could either be absorbed or reflected. If absorbed, it would increase the captured energy within the potential well.
If we regard a photon as simply another particle with a de Broglie vector, then its speed would remain constant because of conservation of momentum. However, a photon passing through a matrix of potential wells, such as a glass medium, would be subject to continuous deceleration and acceleration, thus reducing its average speed.
A mechanism has been proposed to describe the motion and energy of a quantum particle, as observed from any frame of reference, using a single quantum property, the de Broglie vector. The vector and its rotation completely describe the mass and energy of the particle. The mass of the particle is represented by the amplitude of the de Broglie vector and is independent of the frame of reference of the observer. Furthermore, the de Broglie vector provides a possible explanation of the wave particle duality conundrum resulting from quantum mechanics. Its application has been demonstrated for both refraction and reflection. The de Broglie vector also offers a mechanism to account for spin. A logical extension is to assume that matter is nothing more than energy captured within a potential well and that photons could be emitted and absorbed by such a potential well.
[1] Einstein A Ann Phys 17, (1905) 891 - 921
[2] Einstein A Ann Phys 17, (1905) 132-148
[3] Einstein A Ann Phys 18, (1905) 639-641
[4] Feyman R The Character of Physical Law (MIT Press, Cambridge, Mass.) 1967
[5] Mezei F Neutron Spin Echo (Springer, New York) 1980
[6] Michalson A, Morley Am J Sci 34, (1887) 333-345
[7] R J Kennedy and E M Thorndyke Physical Review 42 p400 (1932)
[8] Scharzschild K Sitzber K Preuss 7 (1916) 189-196
[9] Planck M Ann Phys 4