Calculations of de Sitter Apparitions using Revised Relativity

AEA Technology
Current Address: Serco Assurance,
B150, Harwell, Didcot, Oxon., OX11 0QJ, UK

Abstract

Calculations have been carried out, based on the orbits of spectral binary stars reported by Hummel et al. using the Revised Relativity equation for the speed of light. In every case, the systems would not produce de Sitter apparitions unless they were at least two orders of magnitude more distant from the Earth than the measured distance. Calculations on theoretical binary systems have shown that de Sitter apparitions would not occur unless there is a binary system close to the Solar System, which contains a massive star and has a period of rotation of a few hours. No such system has been identified.

1. Introduction

One of the key pieces of evidence for the rejection of corpuscular theory is the absence of de Sitter apparitions in binary systems (see the next section). Special Relativity postulates that the speed of light is constant for all observers. This assumes that electromagnetic radiation is a continuous function. However, the postulates of Quantum Mechanics, supported by observation, maintain that electromagnetic radiation actually takes the form of photons. Howe [1] has proposed a revised equation for relative motion, combining the observed properties for energy change in Newtonian mechanics with those of Special Relativity. This paper sets out to demonstrate that, assuming the revised equation, it is unlikely that de Sitter apparitions could be ever be observed, given the present limits of technology.

2. de Sitter apparitions

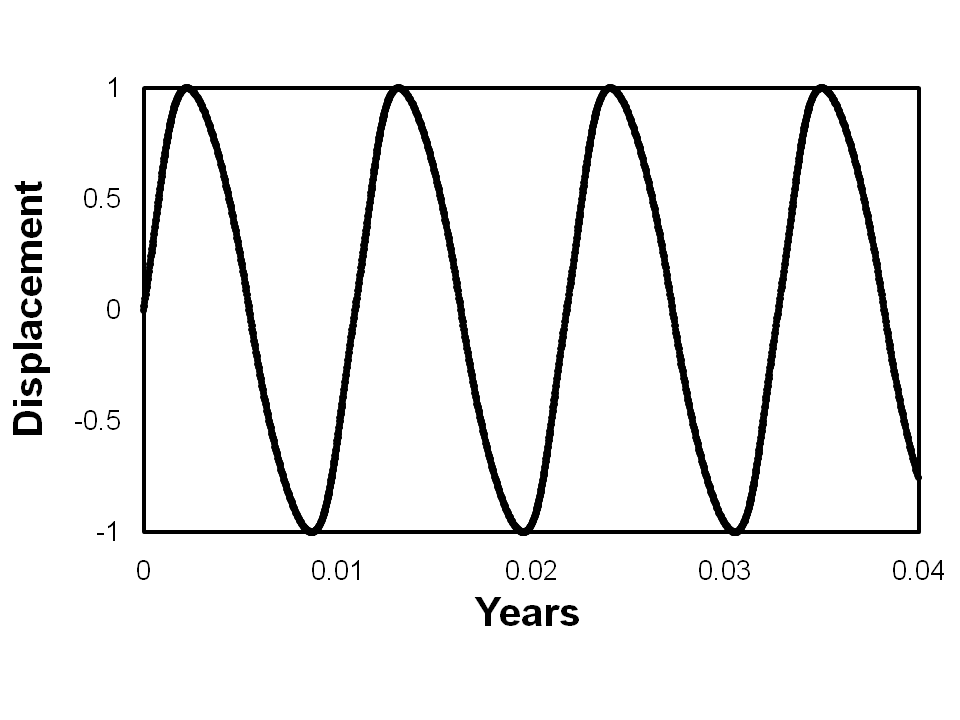
Corpuscular theory postulates that light corpuscles from different parts of a binary orbit would travel towards the Earth at differing speeds. This would result in a distortion of the expected sine wave motion, as shown in Figure 1.

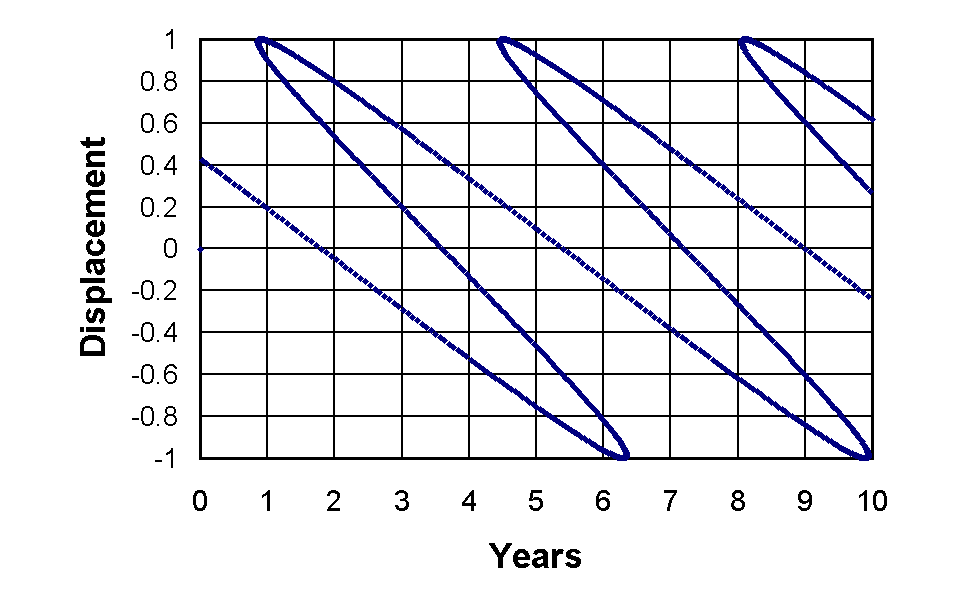
Figure 1: : de Sitter Apparitions would occur because of the postulated speed difference between light corpuscles transmitted when a binary star is approaching the Earth and those transmitted when the star is receding from the Earth. At 5 years and 9 years there would be 5 images, or apparitions, of the star.

In such a case, multiple images, known as de Sitter apparitions, are predicted to occur. No observations of such multiple images have ever been recorded. The absence of de Sitter apparitions in all observations of binary systems is considered as evidence that light travels at a constant speed for all observers. However, this presupposes that the speed of light is additive, i.e. the speed of the corpuscles is equal to the sum of the speed of emitting body and the speed of light, as observed in the frame of reference of that body. Howe's revised equation proposes that the speed of emitted photons is equal to the root sum of the squares of the two speeds. If this equation is assumed, it is still theoretically possible that de Sitter apparitions could be observed, but the distances involved would be much greater, to the extent that it is unlikely that they could ever be resolved.

3. The calculations

Calculations have been carried out on seven spectral binary systems reported by Hummel et. al.[2]. The parameter values used for the calculations are shown in Table 1.

Table 1: Parameter values used for the de Sitter calculations.

The values for mass, period and semi-major axis are taken from Hummel's data. In all cases the star with greatest mass was used, because this produces the most conservative calculation. The radius was calculated using the standard equation:

Where w is in years^-1, M is in solar masses (M) and r is in astronomical units (AU). Distance was calculated using the standard equation:

Where d is in light years (Ly) and a is the semi major axis in milli-arcseconds (mas) (3261 is the conversion factor from kpc to Ly and 1AU/1mas = 1kpc). The distances from standard astronomical tables (e.g. [3]) were used where these indicated a greater distance than the calculations. Distances derived in both ways were reasonably close, but the further distance was used in every case to maintain the most conservative results. The calculations were carried out using Fortran, with the velocity of the star calculated using the standard formula:

Where v is in Ly per year and 1/63240 is the conversion factor from AU to Ly. The component in the direction of Earth was calculated using the normal relationship:

The velocity of the photons was calculated using the revised relativity equation:

Figures 2 to 8 illustrate the results. There is no indication of any de Sitter apparitions for any of the calculations. Indeed, every calculation predicts a motion that is indistinguishable from a sine wave.

Figure 2: Calculated pattern of photons reaching Earth from p-Andromedae.

Figure 3: Calculated pattern of photons reaching Earth from q-Aquilae.

Figure 4: Calculated pattern of photons reaching Earth from b-Aurigae

Figure 5: Calculated pattern of photons reaching Earth from z-Ursae Majoris

Figure 6: Calculated pattern of photons reaching Earth from 93-Leonis

Figure 7: Calculated pattern of photons reaching Earth from b-Tianguli

Figure 8: Calculated pattern of photons reaching Earth from d-Tianguli

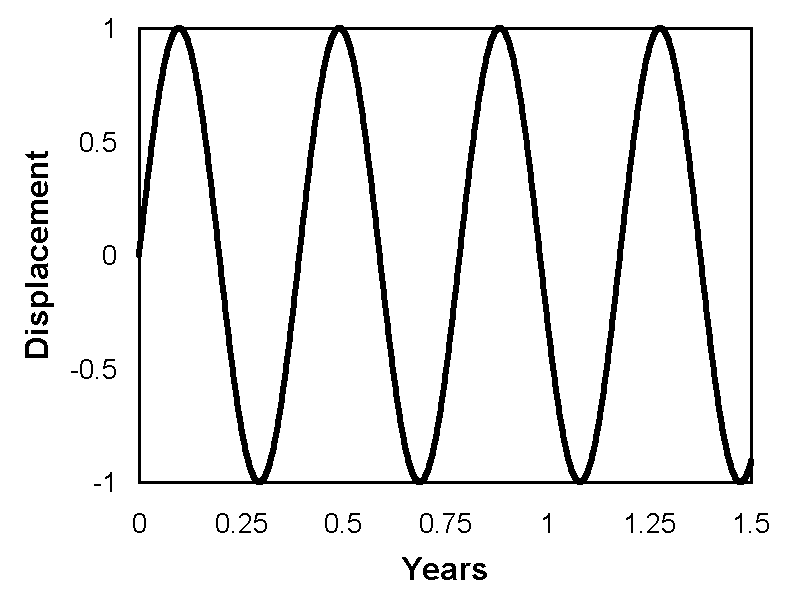
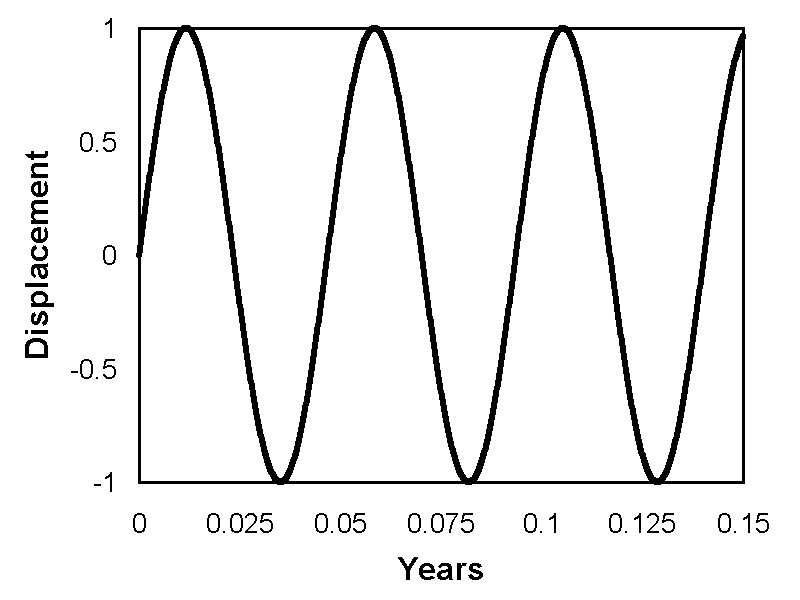
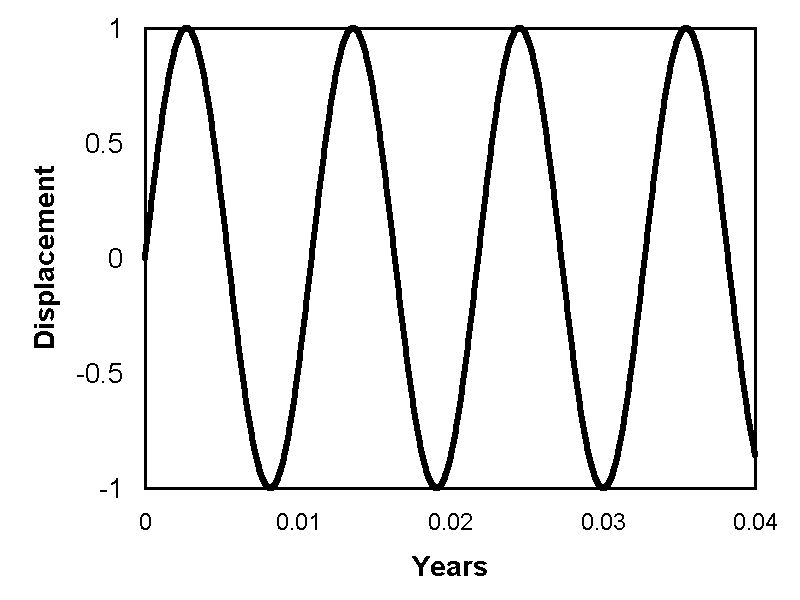
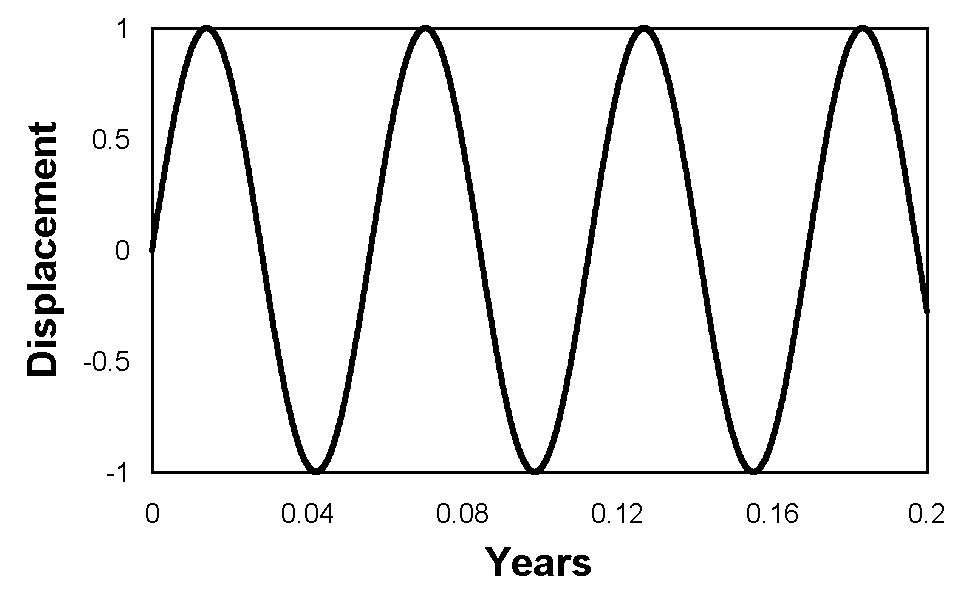
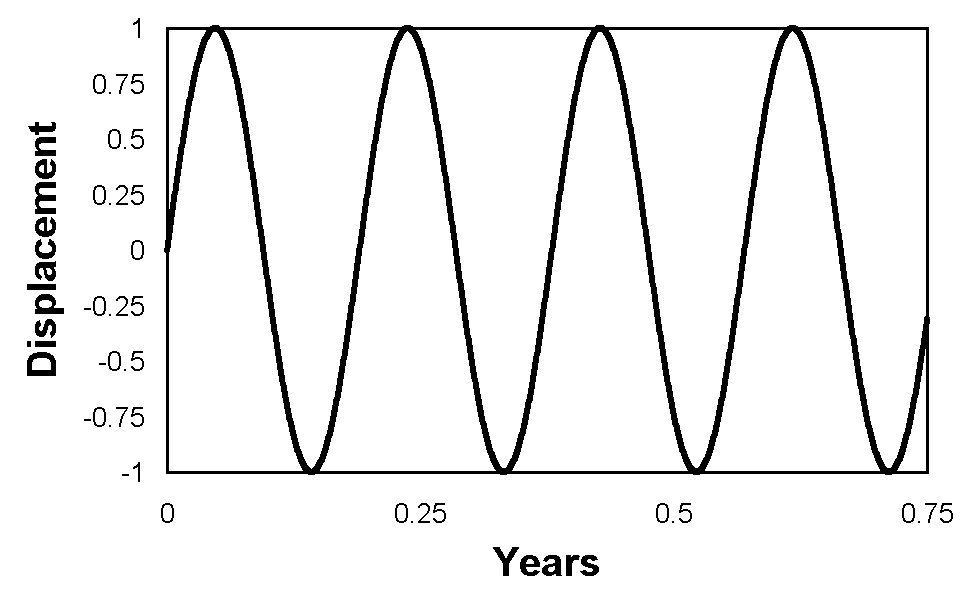
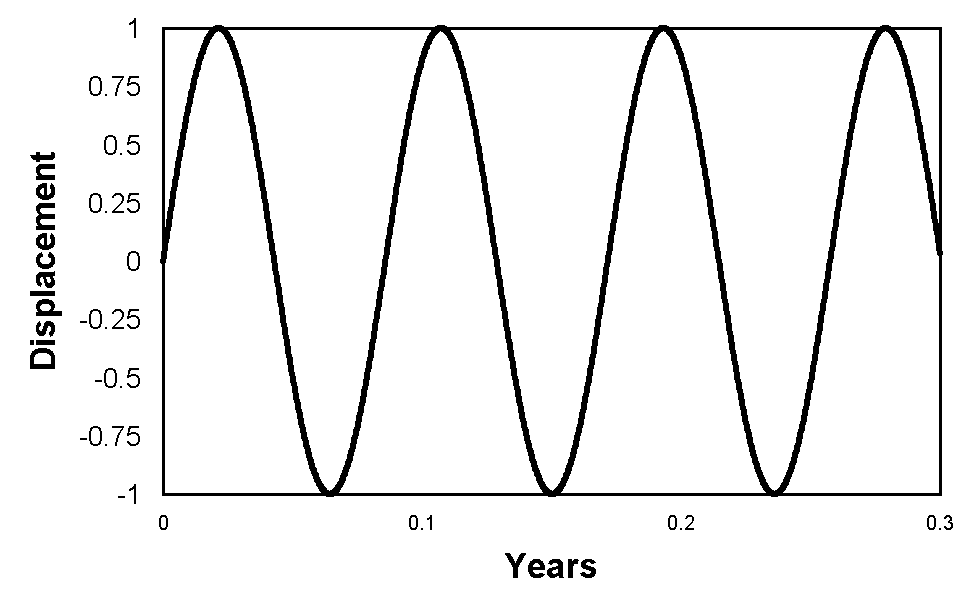
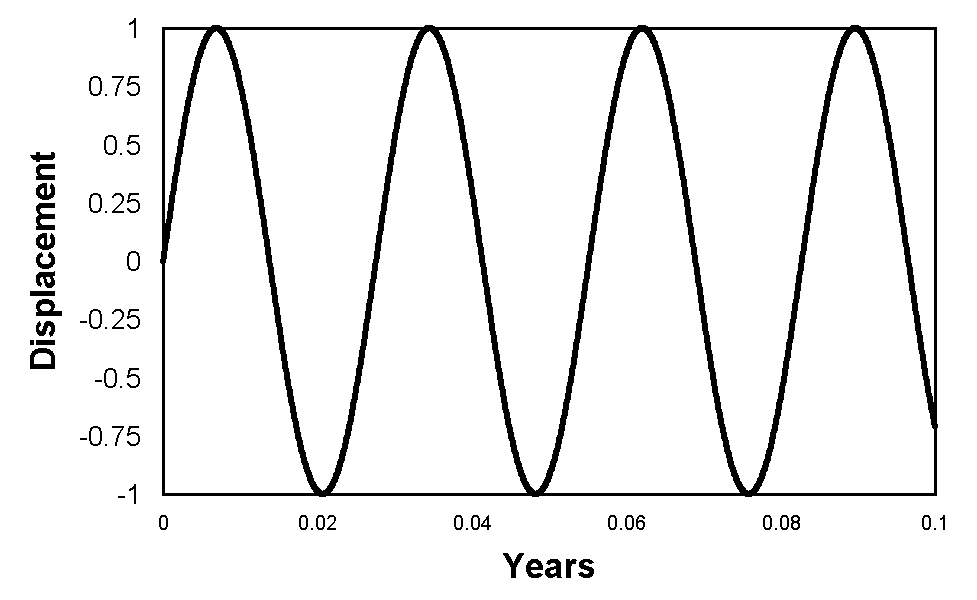
Even more significant is the fact that de Sitter apparitions would not be observed if the stars were more distant than the actual measured distances. In the case of q-Aquilae and b-Aurigae this remained the case for calculations assuming an increase in distance of two orders of magnitude. In all other cases, it remained true for an increase of three orders of magnitude. In most cases, the approximation to a sine wave remained fairly close, but for b-Aurigae, there was considerable distortion, although insufficient to cause de Sitter apparitions, as shown in Figure 9.

Figure 9: Calculated pattern of photons that would reach Earth from b-Aurigae, assuming that the system is two orders of magnitude more distant than the actual measured distance. There is clear distortion from a sine wave, but insufficient to cause de Sitter apparitions. At such a distance the angular resolution of the semi-major axis would be 33 mas, which would be irresolvable.

Considering that all the systems reported by Hummel et al. were spectral binaries, an increase of two or three orders of magnitude would render the systems completely irresolvable, so that it would be impossible to detect any de Sitter apparitions, even if they did occur. Table 2 lists the angular resolution of the systems at the extended distances assumed in the supplementary calculations.

	Calculation distance/Ly	Semi-major axis/mas
p-Andromedae	470000	6.69
q-Aquilae	20300	32
b-Aurigae	6490	33
z-Ursae Majoris	67800	9.64
93-Leonis	192400	7.5
b -Trianguli	122500	10.1
d-Trianguli	25500	8.02

Table 2: Calculations with artificially increased distances showing the associated angular resolutions of the semi-major axes. The angular resolutions are too small to be detected using currently available technology.

4. Theoretical calculations

Theoretical calculations have been carried out to investigate the circumstances in which a binary system might display de Sitter apparitions. If de Sitter apparitions could be predicted by such a calculation, but none were observed from a real system of similar mass, distance and separation, this would be conclusive proof that Howe's Revised Relativity equation is not supportable. In order to demonstrate the range of observable de Sitter apparitions, calculations were performed for a range of stellar masses for 3 values of binary separation. The stellar masses ranged from 100 M down to 0.1 M. The three values of binary separation used were 0.01 AU. 0.1 AU and 1 AU. The results are shown in Figures 9 to 11.

Figure 10: Limit of de Sitter apparitions for a binary separation of 0.01 AU. The vertical line represents an angular resolution for the semi-major axis of 1 mas. The cut-off point is about 33 Ly. Only systems to the right of the oblique line and to the left of the vertical line could be detected.

Figure 11: Limit of de Sitter apparitions for a binary separation of 0.1 AU. The vertical line represents an angular resolution for the semi-major axis of 1 mas. The cut-off point is about 330 Ly. There is only a small, theoretical window for possible detection, to the right of the oblique line and to the left of the vertical line.

Figure 12: Limit of de Sitter apparitions for a binary separation of 1 AU. The vertical line represents an angular resolution for the semi-major axis of 1 mas. The cut-off point is about 3300 Ly. There are no systems to the right of the oblique line and to the left of the vertical line.

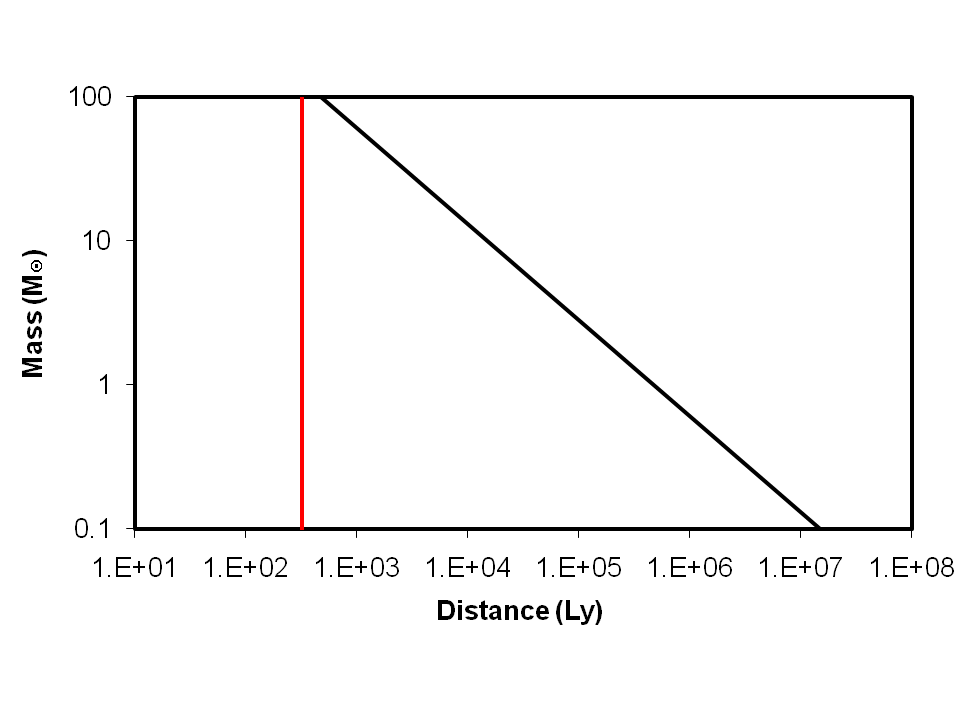
In each of the figures the vertical line represents the limit to the right of which the angular separation of the binary components will be less than 1 mas and, therefore, not resolvable. The oblique line represents the limit for de Sitter apparitions, which would only occur for systems to the right of it. The calculations were performed assuming that de Sitter apparitions occur when the time difference at maximum velocity is greater than one quarter of the period of rotation. From the Figures it can be seen that, for a binary system to display de Sitter apparitions, two criteria must be met. The minimum mass and maximum distances are shown in Table 2, together with the period of rotation.

Table 3: Theoretical calculations of binary systems. The relationship between radius, minimum mass and maximum distance is clearly shown.

This indicates that for a binary system to be a candidate for de Sitter apparitions, it must be close to the Solar System, contain a massive star and have a period of rotation of a few hours. Figure 13 indicates the boundary conditions for such a system, where the radius must be less than 0.16 AU.

Figure 13: Limit of de Sitter apparitions for a binary separation of 0.16 AU. The vertical line represents an angular resolution for the semi-major axis of 1 mas. The cut-off point is about 520 Ly.

Given these constraints, the author has been unable to identify any candidate system for de Sitter apparitions.

5. Conclusions

Calculations have been performed on spectral binary systems to establish whether or not de Sitter apparitions could be possible, using the assumptions of Howe's Revised Relativity equation. It was concluded that de Sitter apparitions could not be produced even if the binary systems were two or three orders of magnitude more distant that the measured distance. At such distances, it would not be possible to resolve the individual stars using current technology. Further calculations have been performed to investigate the conditions under which de Sitter apparitions might be observed. It is concluded that the only circumstances which could lead to de Sitter apparitions is where a binary system close to the Solar System contains a massive star and has a period of rotation of a few hours. No such system has been identified.

References

[1] L D Howe Revised Relativity, www.innovationgame.com/physics (2000).
[2] C A Hummel et al. Astronomical Journal 110 p376 (1995)
[3] Richard Dibon-Smith The Constellations, www.dibonsmith.com/constel.htm (1999)

	Period / days	Mass / M	Radius / AU	Semi-major axis / mas	Distance / Ly
p-Andromedae	143.6	5.8	0.964	6.69	470.0
q-Aquilae	17.123	3.6	0.199	3.2	203.0
b-Aurigae	3.96	2.41	0.066	3.3	64.9
z-Ursae Majoris	20.538	2.55	0.201	9.64	67.8
93-Leonis	71.69	2.25	0.443	7.5	192.4
b-Trianguli	31.39	3.7	0.301	10.1	122.5
d-Trianguli	10.02	0.6	0.077	8.02	25.5

Radius/AU	Minimum Mass/M	Maximum Distance/Ly	Period/Hours
0.01	6.2	33	3.5
0.1	62	330	35
1.0	620	3300	350