1.  Introduction

We have previously considered relativity from the point of energy and matter [1].  This paper was conceived because of the inability of current theories to address this issue.  Essentially there have been three main theories involving the transmission of energy.

2.  Theory 1 - Wave Theory

Wave theory suggested that energy is transmitted through the "Aether" (a medium through which energy waves could propagate).  The key to wave theory is that energy will be transmitted at a constant speed through the ether and that all observers will agree about its speed, taking into account the relative motion of their own frame of reference.  This implies that, in a non-relativistic universe, different values for the speed of light should be measured when the Earth travels at differing speeds in differing directions (because the measured speed should be the addition of the two speeds).  Michelson and Morley carried out an experiment [2] to detect the Earth's motion through the Ether.  However, they were unable to detect any difference in the speed of light when measured in different directions.  Kennedy and Thorndyke [3] later verified that there was no observed change in the measured speed of light when the surface of the Earth travels in different directions.  There have been two alternative theories proposed which satisfy this observation.

3.  Theory 2 - Corpuscular theory

Corpuscular theory assumes that energy is transmitted as corpuscles, tiny packets of energy.  This is in keeping with the ideas of quantum mechanics, which proposes that all energy and sub-atomic phenomena occur as discrete quantifiable "particles", in integer multiples of a base value.  The problem with corpuscular theory is that it predicts that all velocities will be additive, so that in one frame of reference the speed of a corpuscle transmitted from another frame of reference will be the sum of the relative velocity of the frames of reference and the speed of the corpuscle relative to its originating frame of reference.  However, de Sitter [4] suggested observations of binary stars that could support the theory.  He proposed that, given sufficient distance (e.g.  20000 Ly) for certain binary systems, light transmitted when one of the stars was travelling towards the Earth would arrive before light transmitted while the same star was travelling away from the Earth.  This would result in apparitions, several images of the star, some of which appear to move in opposite directions.  All observations of likely stars have failed to provide any such evidence.  Thus corpuscular theory has fallen into disfavour.

4.  Theory 3 - Special Relativity

Before addressing Special Relativity, it is useful here to consider the world of Quantum Mechanics.  Quantum mechanics has proved a very successful description of events on the sub-atomic scale.  It easily extends to energy by proposing that energy is transmitted as photons.  There is much evidence to support this, including the detection of discrete photons in experiments and in astronomical observations.  The problem associated with quantum mechanics arises from the fact that discrete particles behave according to wave theory when considered in large numbers (see e.g. [5]).  We have previously proposed a mechanism for avoiding the need for wave theory for diffraction and refraction [1].  This suggests that quantum mechanics may be able to support an entirely corpuscular model, if the problem of velocity addition can be overcome.

Special Relativity also provides an unsatisfactory explanation of the phenomenon of red shift.  Red shift is observed by astronomers when the motion of stars and galaxies relative to Earth is away from the Earth.  If the speed of light is constant for all observers, the only satisfactory explanation of this phenomenon must rely solely on wave theory.  In wave theory, the interval between successive nodes of the waves is increased because of the relative motion of the emitting body.  In Special Relativity, this effect is accounted for by time dilation.  In both cases, the explanation relies on an increased time interval between successive nodes of a wave train.  The arrival of light as discrete photons is in direct conflict with this hypothesis.  Furthermore, in an earlier paper we have suggested that the energy of a photon is related to its de Broglie frequency.  If this hypothesis is sustained, either the speed of the photon has changed or what we have called its mass equivalence has changed.  However, the mass equivalence is assumed to remain unchanged in all frames of reference.  Hence, using this hypothesis, the speed of a photon would not be constant for all observers

5.  Relativistic Quanta

An attempt has been made to devise a theory that fits with the above noted evidence.  Consider two observers, O and O' respectively, in frames of reference F₀ and F₁, as depicted in Figure 1.

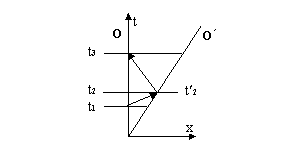
  Assume that O' is moving at a speed u with respect to O.  Assume also that both observers agree that their clocks registered zero at the instant they passed each other.  Consider that the two observers have agreed that O will send a particle to O' with speed v, as observed from F₀ and that, at the instant O' receives the particle, she will send an identical particle to O with speed v as observed from F₁.  Define a function β(v) , such that O' measures the time of arrival t₂ as t'₂ = β(v)t₁.  By relativistic symmetry, t₃ = β(v)t'₂.  So t₃ = β²(v)t₁.

Now

So

and

Also, if O observes the particle sent by O' as having a velocity α(u, v) then

So

Also, if O observes the particle sent by O' as having a velocity α(u, v) then

and

By combining equations 3 and 6 we arrive at

Thus, remembering that t₃ = β²(v)t₁

The time dilation factor γ(u) is t₂/t'₂, so

which simplifies to

Now in a Newtonian world, α(u, v) = - (v - u), so γ(u) = 1.  In the world of Special Relativity, when v = c and α(u, v) = -c we have

giving, as expected

This reveals Equation 10 to be the most general form of the time dilation equation.  The question now arises as to whether or not there is a function for α(u, v) that will satisfy both relativistic and Newtonian observations.  This must include the observation that, in a Newtonian world, observers in different reference frames will disagree about the energy change for the same event.  It must also account for red shift allowing for the constancy of mass equivalence.

We now hypothesise that when v equals the speed of light, c, as observed within a single frame of reference (i.e. when a photon is emitted), all observers will agree on the energy change, mc², where m is the mass equivalence previously postulated[1].  In that analysis, we suggested that the energy of a quantum particle is given by:

Consider the case where a particle is observed by observer O in reference frame in F₀ sent by observer O' in reference frame F₁.  For both observers to agree on the energy change we must have:

Where v is the velocity of the particle relative to O', α(u, v) is the velocity of the particle relative to O and u is the velocity of O' relative to O.  We have chosen to express the velocity of the photon as v for the purpose of subsequent analysis, although in this instance, v = c.  The sign for the "rest" energy in F₁ is +ve for diverging frames because the change in energy is the sum of the rest energy and the resultant energy, whereas it is -ve for converging frames because it is the difference between them.  Equation 14 can be rearranged to reveal the quadratic equation:

Solving for α²(u, v) we arrive at:

Because, in our hypothesis, Equation 16 is only valid when v = c, it can be expressed as:

For u = -0.5c we have α(u, c)= 0.944c.  We can use our previously defined equation for the de Broglie frequency[1] to calculate the red shift:

This implies a red shift of 10.8%, as opposed to the red shift of 13.4% predicted by special relativity.

We now consider the case where both u and v are small relative to c.  In this case α(u, v) = (u + v) so α²(u, v) = (u + v)².  Inserting this value into the form of Equation 16 gives:

Where x is to be determined.  So:

We now have:

This can be expanded to:

or

Rearranging, we arrive at:

It can be seen that if we remove the term 8uv[c² + 2(u + v)² - uv] and allow for the term the term 4(c²u² + u²) to take the sign of u, we arrive at the relativistic Equation 16.  We therefore surmise that relativistic multipliers of the form (1 - v²/c²) are required giving:

So, when v = c and u is significantly less than c, α(u, c) = c , as required by Special Relativity.  On the other hand, where both u and v are significantly less than c, α(u, v) = u + v, as required by Newtonian mechanics.  When v = c and u = 3x10⁴ ms^-1 (approximately the speed of the Earth around the Sun), then the resultant speed of an incident photon would be within 0.5 ms^-1 of the rest value of c.  More than an order of magnitude improvement in the currently available accuracy of the measurement of the speed of light would be required to detect this with any confidence.  If u = c/2 and v = c, α(c/2, c) = 1.05c, significantly less than c/2 + c.

6.  Implications

Using Equation 16a, we have considered [6] seven spectroscopic binaries reported by Hummel et.  al. [7] and, using the above model, found no case where there could be de Sitter apparitions unless the stars were more than 2 orders of magnitude more distant than their measured distance.

There are also implications for red shift.  There is a difference in the calculated red shift compared with Special Relativity, as shown in Figure 2. 

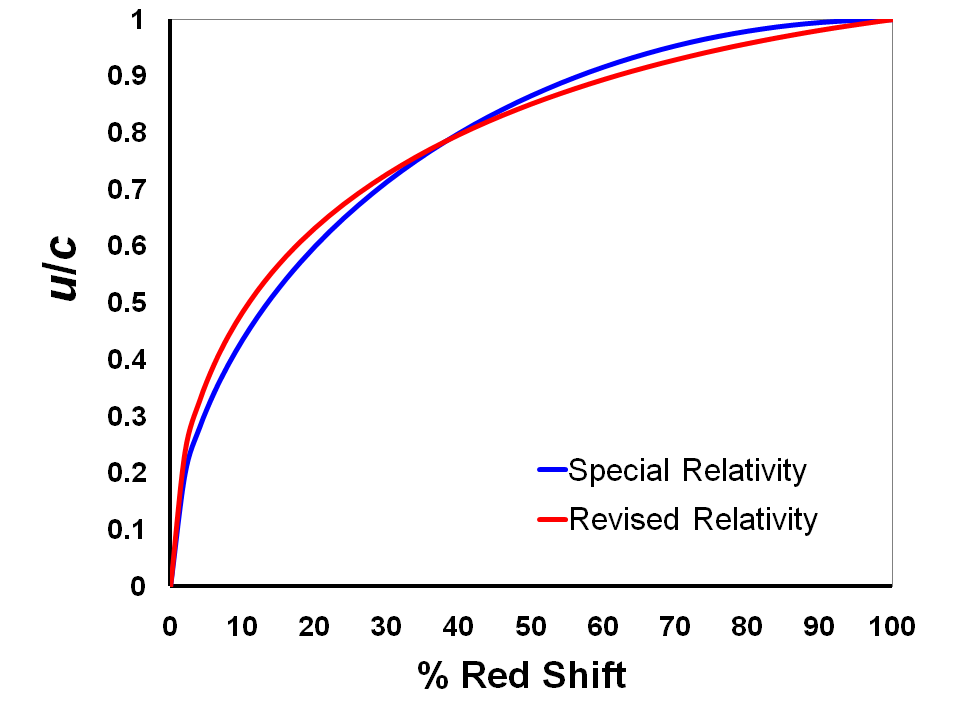
In the case of Special Relativity, from Equation 12, with u = -c/2 and α(u, c) = c, the red shift is related to u, the relative speed of recession of the emitting object, by

whereas for Revised Relativity, from Equation 16 and 17,

It can be seen from the figure that, where there are small red shifts from receding objects, Revised Relativity predicts slightly larger values of u/c than would be expected using the assumptions of Special Relativity.  The situation is reversed when the red shifts are large.  This may have an effect on the estimation of the Hubble constant, H₀, the value of which has been constantly revised over the years.

7.  Conclusions

By considering pre-existing models, a revised model of relativity has been proposed where the speed of light is not constant for all observers.  The model allows for relativistic concepts to be combined with the Newtonian view.  Differences in the measured speed of light are likely to be difficult to detect.  The model satisfies the observation that de Sitter apparitions have not been observed from binary stars.  The value of the Hubble constant may need further revision. 

References

[1] L D Howe On energy, matter and wave-like behaviour, www.innovationgame.com/physics (2000). 
[2] R S Shanckland: American Journal of Physics 32 p16
[3] R J Kennedy and E M Thorndyke Physical Review 42 p400 (1932)
[4] W de Sitter An Astronomical Proof for the Constancy of the Speed of Light, Physik.  Zeitschr. 14, p429, (1913)
[5] R Feynman The Character of Physical Law, MIT Press (1967)
[6] L D Howe Calculations of de Sitter Apparitions using Revised Relativity, www.innovationgame.com/physics(2001)
[7] C A Hummel et al.  Astronomical Journal 110 p376 (1995)