August 2001
This paper sets out to demonstrate that it is possible for photons to have inertia that can be transported to other particles. Using this premise, it is possible to account for the phenomenon of special relativity using quantum mechanical principles. It also proposes that an adaptation of the revised relativity equation can be used to describe relativistic behaviour in a two-particle universe. It is shown that, if photon transport is the means of transferring momentum in an elastic collision, it must obey a constant momentum relationship, rather than a constant energy relationship. If momentum transfer is driven by a constant momentum relationship, there will be a transient energy deficiency, with the energy stored as some form of potential energy during the interaction. The idea of constant momentum transfer agrees with the Galilean concept of relativity. By referring to the momentum of a complete system, rather than that of an individual component, we demonstrate that all observers will agree about energy dissipated, allowing for relativistic effects. The equations for energy deficiency developed for elastic collisions are used to demonstrate this. The principle of momentum transfer by photon transport may help to unify special relativity, quantum mechanical principles and Newtonian mechanics.
We have previously postulated [1] the existence of a de Broglie vector together with a property of photons described as mass equivalence, which for the purpose of this paper, we have termed photon inertia. The De Broglie vector has been used to describe the wave-like properties of quantum particles [1]. A revision of special relativity [2] has developed arguments for the observation of constant energy change for photon emission and absorption by observers in different frames of reference. These two postulations have led to the idea of negative mass [3]. We have further demonstrated, by means of simulation, that photon transport is a feasible means of thermal conduction [4]. This paper develops these ideas further by postulating the transport of momentum by photons.
Reference is made throughout this paper to the photon as the vehicle for the transport of momentum (and therefore energy). However, a theoretical development by Kuijk-Grünbauer [5] proposes that there may be a triplet of such particles, related by parallel laws. These are the photon, the graviton and a hybrid particle. It is not yet clear either what the full inter-relationship between these particles might be, nor what their respective roles would be in the conversion of one type of energy to another. Kuijk Grünbauer has suggested that the graviton may be a more appropriate particle for the transport of momentum. However, until the roles of the various forces are better understood and the concept more widely accepted, the term photon will continue to be used at this juncture. The nomenclature may need to be revised in the light of future theoretical developments.
The hypothesis that photons have negative mass leads naturally to the idea of photon inertia, which is depicted here by the symbol Ip. We use the term particle here to describe a cohesive collection of one or more quantum particles with positive (attractive under gravity) mass. If a photon has negative mass (mutually attractive, but repulsive to positive mass), it will interact with a particle in one of two ways:
In the first case, mutual repulsion, the particle will normally be left effectively undisturbed, because the inertia of the photon will be many orders of magnitude smaller than that of the particle, resulting in elastic scattering. However, in the case where a very low mass particle, such as an electron, interacts with a photon of very high energy, namely a gamma, there may be some energy transfer between the photon and the particle, resulting in observed inelastic scattering.
In the second case, absorption, all of the inertia and momentum will be added to that of the particle. The case where photon momentum and inertia are added to the particle is considered in more detail in the next section. The argument assumes that the absorption of more than one photon will lead to the simple addition of their individual inertias.
In Newtonian terms, the kinetic energy, E, of a moving particle is given by the formula
However, if the photon inertia, Ip, is added to the inertia of the particle this formula becomes
The concept of photon inertia leads to the alternative formula for the kinetic energy of a photon
It can be seen from Equation 3 that Ip is identical to the mass equivalence that we have previously postulated [1]. If the hypothesis of energy transport by photons is accepted, we can equate the post interaction kinetic energy of a particle that was initially at rest with the energy added by photon transport:
Thus
So
Hence
As v approaches c, Ip becomes large, as shown in Figure 1. In the limit of
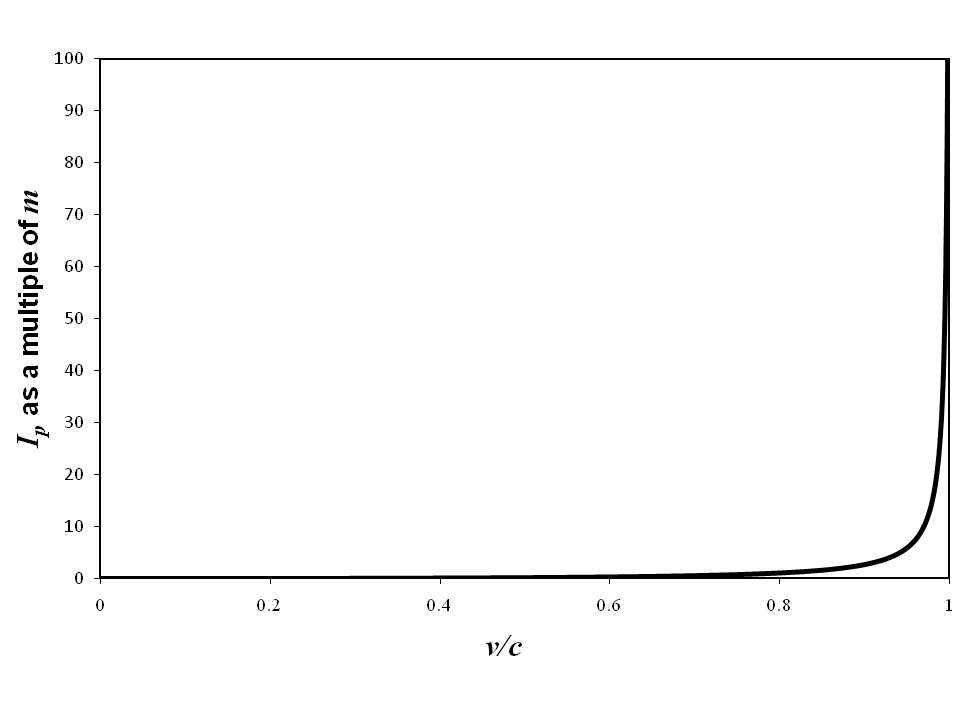
Inserting this value of Ip into Equation 2 and re-arranging gives:
Equation 8 reduces to:
Which can be further simplified to
Equation 9 confirms that light speed cannot be achieved by a particle with non-zero rest mass. Hence we deduce that a photon has zero rest mass, but has inertia (mass equivalence) due solely to its motion.
Consider a universe in which only two particles, A and B, exist and the sole means of energy transport is photons. It is not clear that momentum is conserved a priori. If the theory of energy transport by photons is to be substantiated, it must explain the conservation of momentum during non-relativistic elastic collisions. To understand this, we need to consider the energy transport process as two particles approach one another. Consider the situation where the energy transport process takes place according to some law:
Where dP/dt is the rate of momentum transport with respect to time and f(x) is some function of x, the separation between the particles. To illustrate the above mechanism, Equation 10 has been calculated for two particles in one dimension using
By adding Equations 11 and 12 we get
In other words, the energy transport process defined by Equation 10 results in constant momentum throughout the interaction. It should be noted that the process is entirely independent of the form of f(x) and hence the assumption of the form of f(x) for the purpose of the calculations is perfectly valid. The calculations were performed using FORTRAN, using a time step of
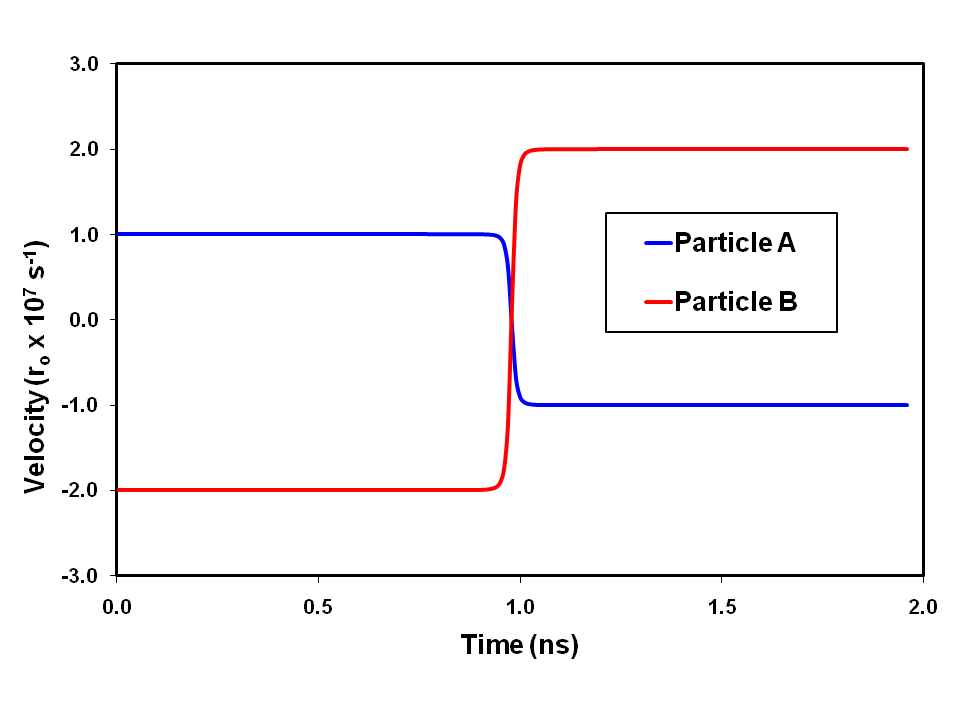
The respective velocities are plotted against separation in Figure 3.
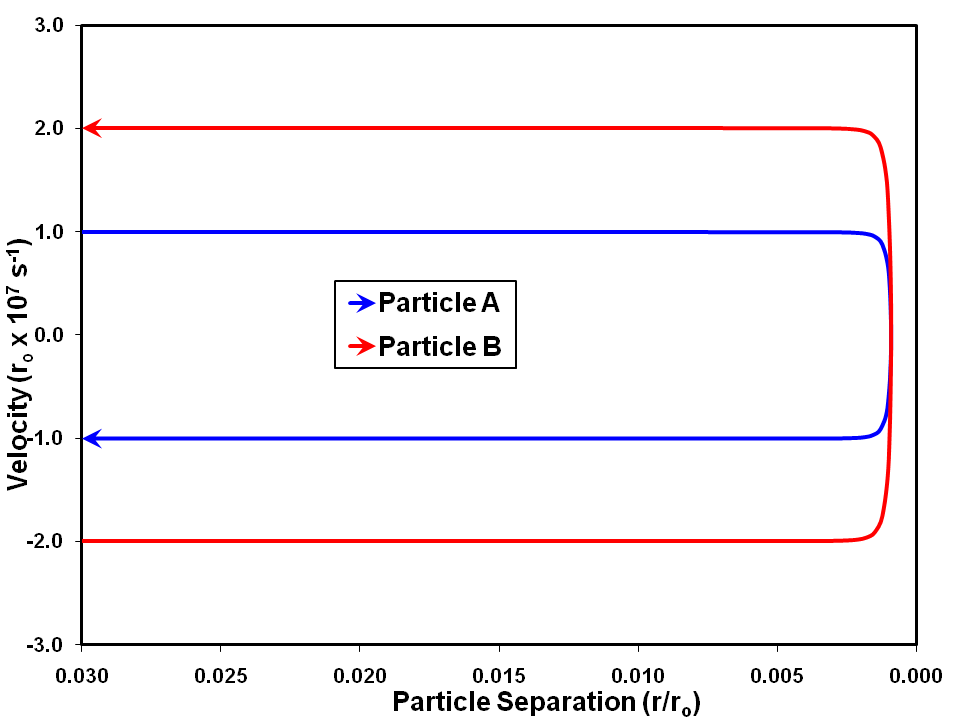
Thus, it can be seen that, using this model, the conservation of momentum in an elastic collision is the consequence of the energy transfer process (although not necessarily a basic law of physics). However, it depends on the assumption that the rate of momentum transfer, rather than the rate of energy transfer, depends on f(x).
Although energy is conserved by the interaction (that is to say
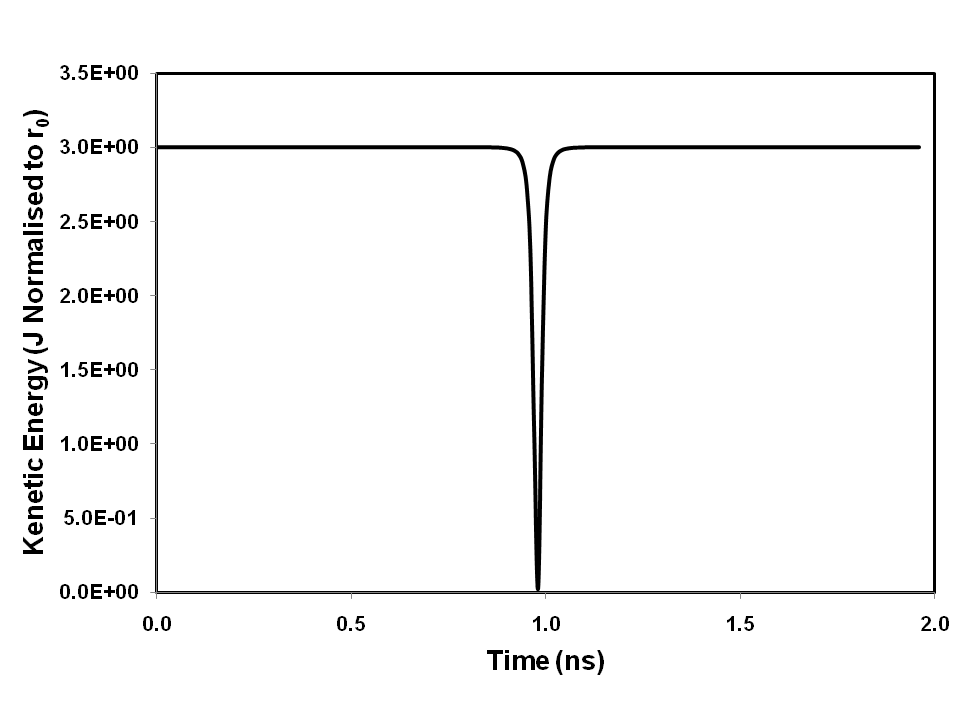
So there is an energy deficiency Ed, at the point of closest approach. This may be regarded as energy locked in the photon transport process.
Let us consider a general case where ma and mb are respectively the masses of the two particles and va and vb are their respective initial velocities. We can write
Equation 14 reduces to:
In the same way, we can write
We now define ζ'r as
So that
From 16 and 18 we get
From this we can see that
Now, the steady-state energy of the system, Emax, when the particles are remote from each other and travelling at constant velocity is given by
Whereas, at the point of closest approach
Substituting 18 into 22 gives
Using 20 for the value of ζ'r we arrive at
By subtracting 24 from 21 we derive the energy deficiency (when the particles are stationary in the frame of reference of the centre of mass).
Equation 25 can be rearranged to give
It can be seen from Equation 26 that Ed depends on
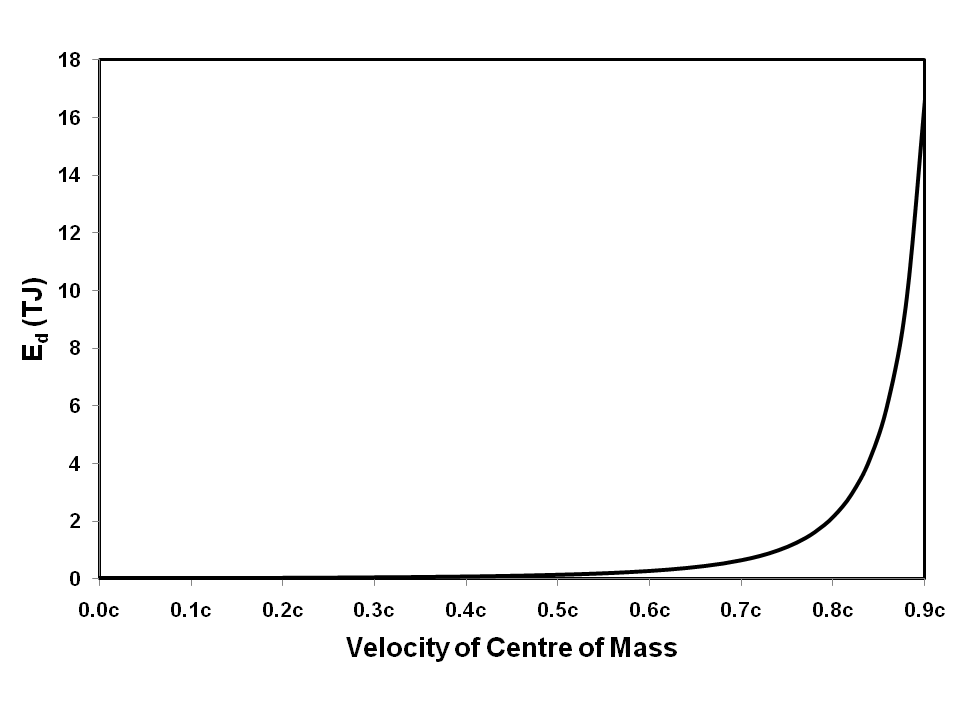
It can be seen that Ed increases rapidly as v/c becomes large. Even if the velocity difference between Pa and Pb is reduced by several orders of magnitude, the percentage increase in Ed remains essentially unchanged for large increases in the relative velocity of the centre of mass. Thus it can be deduced that the frame of reference of the centre of mass is the "natural" reference frame for calculations involving momentum transfer by photons.
The concept of momentum transfer by photon transport fits very well with the concept of the de Broglie vector. From
If we hypothesise that the de Broglie vector rotates in a plane normal to the direction of momentum transfer, the direction of rotation will determine the direction of momentum transfer and the amplitude of the vector is related to Ip, the inertia of the photon, while the rotational velocity is c, the same as the linear velocity of the photon. Thus the de Broglie vector completely describes the momentum transfer process (and hence the energy transfer).
One of the consequences of assuming momentum transfer, as opposed to energy transfer, is that the process can be considered as bi-directional. That is to say, Particle A transferring positive momentum to Particle B is equivalent to Particle B transferring negative momentum to Particle A. This means that the concept of Galilean relativity is maintained.
The transient energy deficiency curve of Figure 4 can be explained by assuming that the deficiency in kinetic energy is stored as some form of potential energy, such as strain energy. The precise nature of the transient energy deficiency in an elastic collision is a matter for further investigation. However, in an inelastic interaction, normal energy loss processes, such as heat production, may account for the energy deficiency. We have previously proposed a model for thermal energy transmission by photon transport [6].
By assuming that photons have inertia and that this can be transported to other particles, it is possible to account for the phenomenon of special relativity by quantum mechanical arguments. We have shown that an adaptation of the revised relativity equation [4] can be used to describe relativistic behaviour in a two-particle universe. Calculations have been used to demonstrate that, if photon transport is the means of transferring kinetic energy in an elastic collision, it must obey a constant momentum relationship, rather than a constant energy relationship. In a constant momentum driven kinetic energy transfer, there will be a transient energy deficiency, with the energy stored as some form of potential energy during the interaction. The idea of constant momentum transfer agrees with the Galilean concept of relativity. By referring to the momentum of a complete system, rather than that of an individual component, it is possible to demonstrate that all observers will agree about energy dissipated, with the exception of relativistic effects. The equations for transient energy deficiency developed for elastic collisions prove to be an ideal means of demonstrating this. The principle of momentum transfer by photon transport agrees with special relativity, quantum mechanical principles and Newtonian mechanics.
[1] L D Howe On energy, matter and wave-like behaviour
www.innovationgame.com/physics (Revision 2013)
[2] L D Howe Revised Relativity
www.innovationgame.com/physics (2001)
[3] L D Howe Symmetry Between Gravitational and Electric Forces
www.innovationgame.com/physics (2002)
[6] L D Howe Thermal Conduction by Photon Transport
www.innovationgame.com/physics (2001)
[7] W Kuijk-Grünbauer A re-dimensionalization of Physics conducive to unified fields, reformulations in QED, Relativity and Strong Forces
(Private Communication) (2003)